Paper published in:
Sala, N. (Ed.)
(1999), Atti del Convegno: Bonaventura
Cavalieri alter Archimedes, 27-28 marzo 1998, Comune di Verbania
LE FIGURE SIMILI NELLA
GEOMETRIA DEGLI INDIVISIBILI
DI BONAVENTURA CAVALIERI
Uno studio storico per
un’esperienza didattica
Giorgio T. Bagni
Dipartimento
di Matematica,
Università
di Roma “La Sapienza”
Summary. In this paper the 10th definition given in the first Book of the main work by B. Cavalieri (1598?-1647), Geometria indivisibilibus continuorum nova quadam ratione promota (1635), is studied. This definition can be compared with the 2nd definition given in the 6th Book of Apollonios’ Konika: these definitions are quite similar, but Apollonios’ one is referred only to Conics, so it is superabundant, while Cavalieri’s one is referred to general plane figures and it is not superabundant. Finally, an educational research is briefly presented.
INTRODUZIONE
Molte ricerche sono state dedicate alla personalità scientifica di Bonaventura Cavalieri (1598?-1647)[1] ed alle sue opere principali, tra le quali spicca la Geometria degli indivisibili (l’edizione originale è del 1635; la seconda, postuma migliorata, è del 1653: Geometria indivisibilibus continuorum nova quadam ratione promota, De Ducijs, Bononiae)[2]. Il ruolo di Cavalieri nello sviluppo della matematica del xvii secolo viene spesso primariamente collegato dagli storici della scienza al metodo degli indivisibili (sebbene recenti studî abbiano ripreso il ruolo cavalieriano nell’àmbito della scuola galileiana: Giusti, 1993)[3].
Sarebbe tuttavia riduttivo limitare l’interesse della Geometria degli indivisibili all’introduzione del metodo cavalieriano che ebbe una chiara importanza nella fase preparatoria all’introduzione del calcolo infinitesimale[4]. Gli scritti matematici di Cavalieri rivelano un’impostazione interessante e personale, ad esempio per quanto riguarda la formulazione delle definizioni.

Frontespizio della Geometria indivisibilibus continuorum di
Cavalieri (Bologna, 1635)
LA
DEFINIZIONE DI FIGURE SIMILI
Il Libro I della Geometria degli indivisibili (che fu redatto dall’Autore solo dopo avere scritto i quattro Libri dal II al V) è dedicato alle definizioni ed ai risultati preliminari. Esaminiamo la definizione X in esso contenuta:
“Si chiameranno, in generale, simili [due] figure piane, in ognuna delle quali singolarmente presa possono essere condotte tangenti opposte, e segmenti aventi gli estremi su di esse, che le incontrano secondo il medesimo angolo dalla medesima parte, in modo che, se si conducono comunque linee rette tra le due tangenti opposte, ad esse parallele, secanti i segmenti che incidono le rette tangenti similmente dalla medesima parte, troviamo che le porzioni di queste parallele, nonché delle tangenti opposte, che sono poste dalla medesima parte tra i detti segmenti incidenti, e il perimetro delle figure, prese nel medesimo ordine, hanno tra di loro lo stesso rapporto dei segmenti rettilinei incidenti a dette tangenti, e aventi gli estremi su di esse” (Lombardo Radice, 1989, p. 69).
Riportiamo la figura presente nella citata edizione del lavoro di Cavalieri:
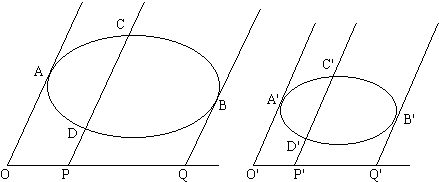
La condizione per la similitudine espressa nella definizione X può essere scritta nel modo seguente[5]. Quando:
OP : O’P’ = OQ : O’Q’
allora risulta:
CP : C’P’ = OQ : O’Q’ e DP : D’P’ = OQ : O’Q’
Il confronto della definizione ora ricordata con alcune classiche definizioni di figure simili è molto interessante.
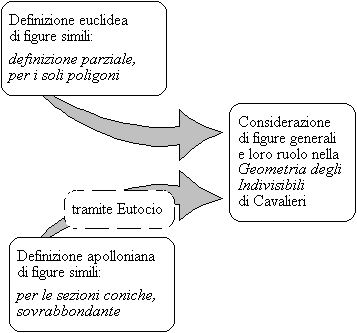
Ad esempio, la definizione esaminata di figure simili è del tutto diversa dalla definizione euclidea (riferita alle sole “figure rettilinee”, introdotte nella definizione XIX del Libro I degli Elementi; modernamente esse corrispondono ai poligoni: Frajese & Maccioni, 1970, pp. 69 e 359):
“Sono figure rettilinee simili quante abbiano gli angoli, uno ad uno, rispettivamente uguali, e proporzionali i lati che comprendono gli angoli uguali”[6].

Il frontespizio degli Elementi euclidei con il commento di
Commandino (Pesaro, 1619)
LA
DEFINIZIONE DI APOLLONIO
Molto interessante è considerare la definizione di similitudine tra sezioni coniche che compare come definizione II del Libro VI delle Coniche di Apollonio:
“Chiamiamo simili [due] sezioni coniche nelle quali, se si conducono rette coniugate a un’asse, in ciascuna delle sezioni, e se si divide ogni asse in un medesimo numero di parti, ovvero in un medesimo rapporto, allora tali rette coniugate sono ordinatamente proporzionali ai segmenti dell’asse da essi staccate a partire dal vertice”[7].
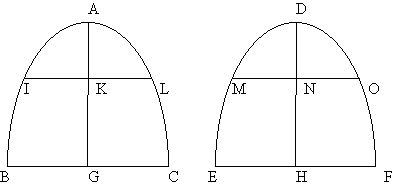
(Nella figura precedente è riportata quella originale in: Apollonio, 1661, p. 135; il lettore potrà constatare che essa sembra riferita a due figure congruenti).

Il frontespizio della prima
edizione dei libri V, VI e VII delle Coniche
(1661)
Non è difficile ravvisare l’analogia di questa definizione con la definizione cavalieriana sopra riportata. Osserviamo tuttavia che l’edizione veneziana del 1537 delle Coniche di Apollonio, a cura di G.B. Memo, era limitata ai soli primi quattro Libri; analogamente per quella bolognese del 1566 dovuta a F. Commandino (Loria, 1929-1933) e per molte edizioni seguenti fino alla metà del xvii secolo (Apollonio, 1655). Al momento della redazione della Geometria degli indivisibili, Cavalieri non poteva conoscere la celebre prima edizione borelliana dei Libri V, VI, VII delle Coniche (Apollonio, 1661), pubblicata a Firenze ben ventisei anni dopo la prima edizione della Geometria degli indivisibili[8].

Il frontespizio
dell'edizione di Anversa (1655) dei primi quattro libri delle Coniche
In uno Scolio immediatamente precedente la definizione X, però, Cavalieri menziona il Libro VI delle Coniche, e riferisce di essersi basato sulla presentazione indiretta data di esso nei Commentarii ad Archimede e ad Apollonio dovuti ad Eutocio di Ascalona (vi secolo d.C.):
“Scolio. Le altre definizioni, quelle date da Euclide di figure piane simili, e solide, e di cilindri e coni simili, e quelle che vengono date da Apollonio, nel libro sesto delle Coniche, di porzioni simili di sezioni di cono, stando a quanto riferisce Eutocio, si prendano così come sono addotte da quegli autori, aggiungendo tuttavia alla definizione di sezioni coniche simili nello stesso luogo data da Apollonio ciò che sarà più avanti detto, se essa verrà applicata agli spazi [racchiusi dalle curve]” (Lombardo Radice, 1989, p. 68).
CONFRONTO
TRA LE DUE DEFINIZIONI
Nello Scolio sopra ricordato, Cavalieri afferma dunque di accettare la definizione di Euclide per i poligoni e quella di Apollonio per le sezioni coniche; solo in un secondo momento, come abbiamo potuto constatare, quest’ultima definizione viene applicata dall’Autore a figure più generali (la corrispondente definizione cavalieriana nel caso di figure solide è la XI: Lombardo Radice, 1989, pp. 74-75).

Il frontespizio degli Elementi euclidei con il commento di
Clavio (Roma, 1603)
A tale proposito, è importante osservare che questa estensione viene ad assumere un significato matematico che va oltre la semplice considerazione di una più ampia classe di figure.
La definizione di Apollonio è infatti chiaramente sovrabbondante se riferita alle sole sezioni coniche: è noto infatti che affinché due coniche siano simili è sufficiente che esse abbiano la stessa eccentricità (si veda ad esempio: Castelnuovo, 1931, pp. 453-454) e dunque in tale caso non risulta necessario imporre la più gravosa condizione espressa nella definizione II del Libro VI delle Coniche.
Nella Geometria degli indivisibili, pertanto, Cavalieri non solo estende consapevolmente l’impostazione di Apollonio alla similitudine di una classe più ampia di figure (e proprio in questa generalità possiamo evidenziare uno dei grandi pregi dell’intera opera cavalieriana, come ben sottolineato in: Lombardo Radice, 1989, p. 70); ma egli, basandosi sull’antica considerazione delle sole sezioni coniche, ne applica correttamente la condizione di similitudine a figure generalmente intese, per le quali la concezione dell’eccentricità sarebbe chiaramente improponibile[9]. In tale modo Cavalieri si mostra in grado di “sfruttare” le potenzialità dell’elegante ed efficace definizione di figure simili data nel Libro VI delle Coniche[10] assai più a fondo di quanto abbia fatto lo stesso Apollonio; e può inoltre così eliminare il carattere di sovrabbondanza di tale importante definizione.
IMPORTANZA
DELLA DEFINIZIONE DI
FIGURE
SIMILI NELLA GEOMETRIA DEGLI INDIVISIBILI
La definizione X del Libro I della Geometria degli indivisibili, precedentemente analizzata, assume un’importanza fondamentale nello sviluppo del trattato di Cavalieri. La nozione di figure simili (piane e solide) viene infatti ripresa in termini spesso decisivi nel corso di tutto il lavoro cavalieriano.
Interessante, a tale proposito, è il compendio della Geometria degli indivisibili proposto da Paolo Frisi nell’Elogio di Bonaventura Cavalieri (Frisi, 1825; la dedica dell’Autore a Pietro Verri porta la data del 20 marzo 1778):
“Ecco il prospetto di tutta la Geometria degl’Indivisibili. Nel primo libro, e in una porzione del secondo, incomincia il Cavalieri a trattare di quelle quantità, in cui tutti gli elementi analoghi hanno tra loro la stessa proporzione. Il suo lungo ragionamento si ridurrebbe sostanzialmente a questa semplice proporzione: Che tutte le figure, i cui elementi crescono o scemano similmente dalla cima alla base, sono alla figura uniforme della base medesima e della medesima altezza nella proporzione costante, con cui gli elementi crescono o scemano. Il Cavalieri... ha fatto vedere come [a ciò] si riduca una gran parte della Geometria degli antichi” (Frisi, 1825, pp. 209-210).

Il frontespizio di Operette scelte di Frisi (Milano, 1825;
la dedica è del 20 marzo 1778),
in cui è incluso l'Elogio di Bonaventura Cavalieri
Già nel Libro I, infatti, Cavalieri dedica un’Appendice prima alla “spiegazione dell’antecedente definizione X” (Lombardo Radice, 1989, pp. 72-74; un’analoga Appendice seconda è dedicata alle figure solide, pp. 76-79). Poco oltre, l’Autore conferma in uno Scolio di essere consapevole dell’importanza della generalizzazione introdotta per la similitudine delle figure piane (e solide):
“Scolio. Per quel che concerne il nome di figure simili, è da avvertire peraltro che, quando chiamo simili figure piane, o solide, io intendo, con ciò per esse le definizioni generali sopra allegate; quando invece le chiamo con nomi particolari, intendo le definizioni particolari da altri, o da me allegate per la loro similitudine; così, quando dirò porzioni simili di sezioni di cono, intenderò la loro definizione particolare, e quando dirò parallelogrammi simili intenderò riferirmi alla definizione particolare di figure rettilinee [poligoni] simili, e così in altri casi, giacché più sotto dimostreremo che dalle medesime figure sono verificate ambedue le definizioni, sia la particolare che la generale” (Lombardo Radice, 1989, p. 79)[11].
Alcuni risultati di seguito presentati sono esplicitamente collegati alla similitudine (ad esempio le proposizioni XI, XII, XIII, XIX, XX, XXI, XXII); rispetto alle concezioni classiche (di Euclide e di Apollonio), l’Autore si riferisce ad un’impostazione ben più ampia, in quanto nella trattazione euclidea, ad esempio “si parla solo di coni in senso elementare e non di solidi conici nell’accezione (più generale) di Bonaventura Cavalieri” (Lombardo Radice, 1989, p. 113)[12].
Anche nei Libri successivi del trattato la nozione di figure simili si mantiene fondamentale: già nel Libro II, centrale per la precisazione del metodo degli indivisibili, la definizione VIII è dedicata all’introduzione di “tutte le figure simili” rispetto ad una figura assegnata (Lombardo Radice, 1989, pp. 195-196).
Un completo esame dello sviluppo del trattato cavalieriano esula dagli scopi del presente lavoro; quanto sopra osservato ci consente tuttavia di concludere che la generalità conferita da Cavalieri alla nozione di figure simili con la definizione X del Libro I anticipa e riflette la pregevole, essenziale generalità di tutta la Geometria degli indivisibili e, in ultima analisi, del metodo degli indivisibili.

Il frontespizio della prima
edizione di Opuscula Mathematica
(Venezia, 1575) di Maurolico
UN’ESPERIENZA DIDATTICA
Considerazioni come le precedenti possono avere alcune interessanti ricadute in ambito didattico[13]. Le definizioni di figure simili di Apollonio-Cavalieri e di Euclide riflettono evidentemente due concezioni epistemologiche ben diverse, la cui importanza didattica può essere valutata sperimentalmente.
La necessità di un’attenta storicizzazione delle concezioni epistemologiche della geometria è ad esempio sottolineata da E. Barbin:
“Ogni lettura suppone una re-interpretazione ed ogni scrittura suppone una ri-appropriazione di idee o di conoscenze. Le re-interpretazioni e le ri-appropriazioni del sapere geometrico attraverso le opere di geometria elementare corrispondono... a delle concezioni epistemologiche. Ma queste concezioni devono essere, esse stesse, situate nel loro contesto storico” (Barbin, 1994, p. 157; la traduzione è nostra)[14].
Un’esperienza didattica, tuttora in corso, riguarda l’influenza delle diverse impostazioni geometriche nell’apprendimento di alcuni concetti fondamentali (A. Gagatsis, Università di Cipro, e G.T. Bagni). In particolare, abbiamo voluto esaminare, mediante un test, se una prima presentazione della similitudine di triangoli condotta mediante la definzione di Euclide viene ad essere più chiara ed efficace di un’analoga presentazione condotta attraverso la definizione (più generale) di Apollonio-Cavalieri.
Illustreremo brevemente tale ricerca (ci siamo basati su alcune precedenti esperienze; ad esempio: Demetriadou & Gagatsis, 1995; Gagatsis & Thomaidis, 1995; si veda inoltre: Hoffer, 1981).
Ai 98 allievi di quattro classi della Scuola Media (II corso, allievi di 12-13 anni), a Treviso, Italia, sono stati proposte due schede. Le classi sono state divise in due gruppi, a caso, di 49 allievi ciascuno (li indicheremo come: gruppo A e gruppo A): la seguente scheda A è stata fornita agli allievi del gruppo A, la seguente scheda B agli allievi del gruppo B.
Al momento del test, gli allievi conoscevano le nozioni basilari della geometria euclidea e le nozioni di rapporto e di proporzione. Non avevano ancora trattato la geometria delle coordinate. Particolarmente importante è sottolineare che essi non avevano ancora trattato la similitudine.
Scheda A
(Apollonio-Cavalieri)
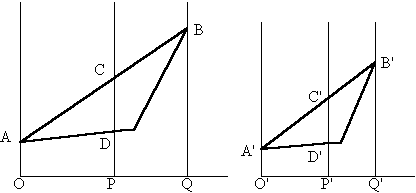
Le rette AO, CP, BQ sono parallele e sono perpendicolari alla retta OQ. Le rette A’O’, C’P’ e B’Q’ sono parallele e sono perpendicolari alla retta O’Q’.
Scegli le rette passanti per P e per P’ come vuoi, in modo però che il rapporto tra OP e O’P’ sia uguale a quello tra OQ e O’Q’ (ad esempio, se OQ = 2O’Q’, deve essere OP = 2O’P’). Sai allora che:
- il rapporto tra CP e C’P’ è uguale al rapporto tra OQ e O’Q’ (nell’esempio: CP = 2C’P’);
- il rapporto tra DP e D’P’ è uguale al rapporto tra OQ e O’Q’ (nell’esempio: DP = 2D’P’).
Che cosa puoi dire dei triangoli nella figura?
Scheda B (Euclide)
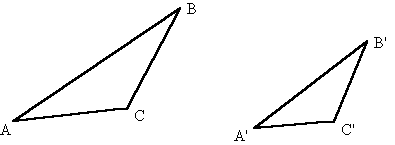
Il rapporto tra AB e A’B’ è uguale al rapporto tra AC e A’C’ ed è uguale a quello tra BC e B’C’ (ad esempio, se è AB = 2A’B’, è anche AC = 2A’C’ ed è BC = 2B’C’).
Per quanto riguarda gli angoli interni dei triangoli, sai che:
- l’angolo in A è congruente all’angolo in A’;
- l’angolo in B è congruente all’angolo in B’;
- l’angolo in C è congruente all’angolo in C’.
Che cosa puoi dire dei triangoli nella figura?
Tempo accordato: 5 minuti (abbiamo voluto che gli allievi esaminassero il problema velocemente, quasi “a colpo d’occhio”).
Non è stato consentito l’uso di libri di testo o di appunti.
Risultati
del test: scheda A
Le risposte fornite dagli allievi possono essere ricondotte alle seguenti:
Sono uno il doppio dell’altro
(prevedibile riferimento al caso particolare dell’esempio) 21 43%
Uguali (congruenti) 1 2%
Diversi (più piccolo e più grande etc.) 11 22%
Hanno la stessa forma (in scala etc.) 11 22%
Nessuna risposta 5 11%
Risultati
del test: scheda B
Le risposte fornite dagli allievi possono essere ricondotte alle seguenti:
Sono uno il doppio dell’altro
(prevedibile riferimento al caso particolare dell’esempio) 18 37%
Uguali (congruenti) 0 0%
Diversi (più piccolo e più grande etc.) 6 12%
Hanno la stessa forma (in scala etc.) 14 29%
Nessuna risposta 11 22%
Riassumiamo i risultati nella figura seguente (che fornisce soltanto una rappresentazione qualitativa).
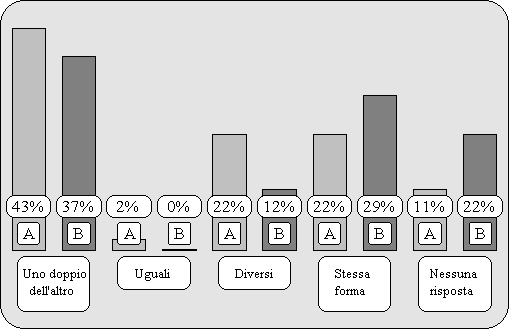
Rileviamo innanzitutto che l’esiguità del campione (il quale peraltro non è stato individuato mediante criterî di rilevanza statistica) non consente ancora la formulazione di considerazioni aventi validità generale.
Possiamo comunque notare che, indicativamente, l’approccio intuitivo alla similitudine basato sulla definizione di Apollonio-Cavalieri e quello basato sulla definizione di Euclide appaiono pressoché equivalenti (e ciò accade nonostante la constatata maggiore generalità della definizione di Apollonio-Cavalieri): la differenza delle percentuali delle risposte che fanno riferimento alle figure simili (22% per la scheda A e 29% per la scheda B) è infatti troppo esigua per poter essere considerata rilevante.
Alcuni allievi sono stati intervistati (singolarmente, ma alla presenza dei compagni, in classe). Le giustificazioni fornite non rivelano sostanziali differenze tra i gruppi A e B. Esse rivelano comunque una netta influenza dell’esempio proposto: 47 allievi (il 48% del totale dei due gruppi A e B) hanno fatto esplicito riferimento al caso particolare (tale tendenza era evidente anche dall’esame preliminare dei risultati: il 40% degli allievi ha affermato che i due triangoli considerati sono uno il doppio dell’altro). Tra coloro i quali hanno riconosciuto che i due triangoli hanno la stessa forma, 19 allievi su 25 (il 19% del totale dei due gruppi A, B) hanno fatto riferimento alla figura.
Ulteriori e più precisi risultati potranno essere ottenuti considerando campioni più significativi e predisponendo test più organici, la cui analisi sia condotta anche sulla base di interviste approfondite. Sarà inoltre opportuno esaminare, con riferimento ai superiori livelli scolastici, l’influenza dello studio dei vettori e della geometria delle coordinate.

La statua di Cavalieri a
Brera (Milano), dall'Elogio di B. C.
di Gabrio Piola (1844)
Riferimenti
bibliografici
Agostini, A. (1925), I concetti di limite e di integrale in un allievo di Cavalieri, Bollettino U.M.I., 4. Altri lavori dello stesso Autore sono dedicati all’opera di Mengoli.
Andersen, K. (1985), Cavalieri’s method of indivisibles, Archive for history of exact sciences, 31, 291-367.
Apollonio (1655), Apollonii Pergaei Conicorum Libri IV. Cum commentariis R.P. Claudii Richardi, Verdussen, Antwerpiae.
Apollonio (1661), Apollonii Pergaei Conicorum Lib. V, VI, VII, paraphraste Abalphato Asphahanensi... Abrahamus Ecchellensis Maronita... lat. reddidit, Io: Alfonsus Borellus... curam in geom. vers. contulit, Cocchini, Firenze.
Arrighi, G. (1973), La Geometria indivisibilibus continuorum di Bonaventura Cavalieri nella ritrovata stesura del 1627, Physis, XV, 133-147.
Bagni, G.T. (1992), Una breve storia “Delle matematiche applicate” (1808) di Francesco Maria Franceschinis, La matematica e la sua didattica, VI, 2, 28-32.
Bagni, G.T. (1996), Storia della Matematica, I-II, Pitagora, Bologna.
Barbieri, F. & Pepe, L. (a cura di) (1992), Bibliografia italiana di storia delle matematiche 1961-1990, Bollettino di storia delle matematiche, XII, 1 (giugno 1992).
Barbin, E. (1988), La démonstration mathématique: significations épistémologiques et questions didactiques: Bulletin de l’APMEP, 366. Inoltre: La dimostrazione matematica: significati epistemologici e questioni didattiche: Quaderni di lavoro n. 10, Istituto Filippin, Paderno del Grappa.
Barbin, E. (1991), La démonstration mathématique: histoire, épistémologie et enseignement: Actes des 2èmes journées Paul Langevin, Université de Brest.
Barbin, E. (1994), Sur la conception des savoirs géométriques dans les Éléments de géométrie: Gagatsis, A. (1994), Histoire et enseignement des Mathématiques: Cahiers de didactique des Mathématiques, Thessaloniki, 14-15, 135-158.
Baron, M.E. (1969), The origin of the infinitesimal Calculus, Pergamon Press, Oxford.
Baroncelli, G. (1987), (Bonaventura Cavalieri) Carteggio, Olschki, Firenze.
Bortolotti, E. (1928), Studi e ricerche sulla storia della matematica in Italia nei secoli xvi e xvii, Zanichelli, Bologna.
Bortolotti, E. (1947), La storia della matematica nella Università di Bologna, Zanichelli, Bologna.
Bos, H.J.M. (1975), Differentials, high-order differentials and the derivative in the Leibnizian calculus, Archive for History of Exact Sciences, 14, Springer-Verlag, Berlin-Heidelberg-New York, 1-90.
Bottazzini, U. (1987), La rivoluzione galileiana a Bologna: Bonaventura Cavalieri, Storia illustrata di Bologna. I novecento anni dell’Università, 8/VI, 141-160, AIEP, San Marino.
Bottazzini, U. (1988), Antichi paradigmi e nuovi metodi geometrici: Rossi, P. (a cura di), Storia della scienza moderna e contemporanea, I, 129-162, UTET, Torino.
Bottazzini, U. (1990), Il flauto di Hilbert. Storia della matematica moderna e contemporanea, UTET, Torino.
Bottazzini, U.; Freguglia, P. & Toti Rigatelli, L. (1992), Fonti per la storia della matematica, Sansoni, Firenze.
Bourbaki, N. (1963), Elementi di storia della matematica, Feltrinelli, Milano (Eléments d’histoire des mathematiques, Hermann, Paris 1960).
Boyer, C. (1969), The History of the Calculus, in: Hallerberg et. al. (1969), Historical Topics for the Mathematics Classroom, Nat. Council of Teachers of Mathematics, Washington.
Boyer, C.B. (1982), Storia della matematica, Mondadori, Milano (A History of Mathematics, John Wiley & Sons, New York 1968).
Calinger, R. (a cura di) (1996), Vita mathematica: historical research and integration with teaching, Mathematical Association of America.
Carruccio, E. (1971), Cavalieri: Gillespie, C.C. (a cura di), Dictionary of Scientific Biography, III, 149-153, New York.
Carruccio, E. (1972), Matematiche elementari da un punto di vista superiore, Pitagora, Bologna.
Castelnuovo, G. (1931), Lezioni di geometria analitica, Società Anonima Editrice Dante Alighieri, Milano-Genova-Roma-Napoli.
Castelnuovo, G. (1938), Le origini del calcolo infinitesimale, Zanichelli, Bologna (ristampa: Feltrinelli, Milano 1962).
Cavazza, M. (1979-1980), L’“oscurità” di Pietro Mengoli e i suoi difficili rapporti con i contemporanei, Memorie dell’Accademia delle Scienze dell’Istituto di Bologna, Classe di Scienze Morali, 74, LXXVII.
Cioffarelli, G. (1982), Su La sfera armillare, manoscritto di Cavalieri: Montaldo, O. & Grugnetti, L. (a cura di), La storia delle matematiche in Italia, Università di Cagliari, Cagliari, 425-430.
Clavio, C. (1603), Euclidis Elementorum Libri XV, apud Aloysium Zannettum, Roma (quarta edizione; la prima edizione degli Elementi commentati da Clavio è del 1574).
Commandino, F. (1619), Euclidis Elementorum Libri XV, Typis Flaminij Concordiae, Pesaro (prima ed. latina: Pesaro, 1572; trad. italiana: Urbino, 1575).
Conforto, F. (1948), L’opera scientifica di Bonaventura Cavalieri e di Evangelista Torricelli, Atti del Convegno di Pisa, 23-27 settembre 1948, Ministero della P.I., Direzione Generale per l’Istruzione Tecnica.
Demetriadou, H. & Gagatsis, A. (1995), Teaching and learning problems on the concept of vector in Greek secondary education: Gagatsis, A. (a cura di), Didactics and history of mathematics, Erasmus ICP 94-G-2011/11, Thessaloniki.
Dupont, P. (1981), Appunti di storia dell’analisi infinitesimale. I. Le origini. II, p. II. Newton e Leibniz. Cortina, Torino.
Edwards, C.H. Jr. (1994), The Historical Development of the Calculus, Springer Verlag, Berlin (3rd printing, 1st ed.: 1979).
Eneström, G. (1912), Zur Geschichte der unendlichen Reihen in die mitte des siebzehnten Jahrhunderte, Biblioteca Matematica, 135-148.
Enriques F. (1930), Gli Elementi di Euclide e la critica antica e moderna Zanichelli, Bologna.
Enriques, F. (1938) Le matematiche nella storia e nella cultura, Zanichelli, Bologna (ristampa anastatica: Zanichelli, Bologna 1982).
Fauvel, J. (1990), History in the mathematical classroom: The IREM papers, The Mathematical Association.
Fauvel, J. (1991), For the learning of mathematics (numero speciale sull’impiego della storia della matematica nell’insegnamento), 11, 2.
Fauvel, J. & van Maanen, J. (1997), Storia e didattica della matematica: Lettera Pristem, 23, 8-13.
Favaro, A. (1885), Bonaventura Cavalieri nello Studio di Bologna, Fava e Garagnani, Bologna.
Frajese, A. & Maccioni, L. (1970), Gli Elementi di Euclide, UTET, Torino.
Franceschinis, F.M. (1808), Delle matematiche applicate, Nicolò Zanon Bettoni, Padova.
Freguglia, P. (1982), Fondamenti storici della geometria, Feltrinelli, Milano.
Frisi, P. (1825), Elogio di Bonaventura Cavalieri, Operette scelte, Silvestri, Milano, 183-248.
Furinghetti, F. (a cura di) (1992), Definire, argomentare e dimostrare nel biennio e nel triennio: opinioni, esperienze e risultati di ricerche a confronto, Atti del secondo Internucleo della Scuola secondaria superiore, Progetto strategico del CNR: Tecnologie e innovazioni didattiche, Quaderno n. 13.
Furinghetti, F. (1993), Insegnare matematica in una prospettiva storica: L’educazione matematica, III, IV, 123-134.
Furinghetti, F. & Somaglia, A. (1997), Storia della matematica in classe, L’educazione matematica, XVIII, V, 2, 1.
Gagatsis, A. & Thomaidis, J. (1995), Eine Studie zur historischen Entwicklung und didactischen Transposition des Begriffs “absoluter Betrag”: Journal für Mathematik-Didactik, 16, 1/2, 3-46.
Geymonat, L. (1947), Storia e filosofia dell’Analisi infinitesimale, Levrotto e Bella, Torino.
Giuntini, S.; Giusti, E. & Ulivi, E. (1985), Opere inedite di Bonaventura Cavalieri, Bollettino di Storia delle scienze matematiche, V, 1-2, 3-352.
Giusti, E. (1980), Bonaventura Cavalieri and the theory of indivisibles, saggio introduttivo a: Cavalieri, B., Exercitationes geometricae sex, rist. anastatica, U.M.I., Cremonese, Roma.
Giusti, E. (1982), Dopo Cavalieri. La dicussione sugli indivisibili: Montaldo, O. & Grugnetti, L. (a cura di), La storia delle matematiche in Italia, Università di Cagliari, Cagliari, 85-114.
Giusti, E. (1993), Euclides reformatus. La teoria delle proporzioni nella scuola galileiana, Bollati Boringhieri, Torino.
Grugnetti, L. (1992), L’histoire des mathématiques: une expérience interdisciplinaire fondée sur l’histoire des mathématiques, Plot, 60, 17-21.
Hanna, G. (1997), Il valore permanente della dimostrazione: La matematica e la sua didattica, 3, 236-252.
Hoffer, G. (1981), Geometry is more than proof: Mathematics teacher, 74, 1, 11-18.
Kline, M. (1982), La matematica nella cultura occidentale, Feltrinelli, Milano (Mathematics in western culture, Oxford University Press, New York 1953).
Kline, M. (1991), Storia del pensiero matematico, I-II, Einaudi, Torino (edizione originale: Mathematical thought from ancient to modern times, Oxford University Press., New York, 1972).
Koyré, A. (1973), Bonaventura Cavalieri et la géometrie des continus, Études d’histoire de la pensée scientifique, Gallimard, Paris.
Lombardo Radice, L. (1989), Geometria degli indivisibili di Cavalieri, UTET, Torino (la prima edizione è del 1966).
Loria, G. (1929-1933), Storia delle matematiche dall’alba delle civiltà al tramonto del secolo XIX, Sten, Torino (ried.: Hoepli, Milano 1950; ristampa anastatica: Cisalpino-Goliardica, Milano 1982).
Maracchia, S. (1992), Luca Valerio matematico Linceo: Conti, L. (a cura di), La matematizzazione dell’universo. Momenti della cultura matematica tra ‘500 e ‘600, 253-302, Università degli studi di Perugia, Porziuncola, Assisi.
Matteuzzi, M. (1979-1980), Pietro Mengoli e l’algebra della logica, Memorie dell’Accademia delle Scienze dell’Istituto di Bologna, Classe di Scienze Morali, 74, LXXVII.
Maurolico, F. (1575), De lineis horarijs libri tres, Francisci Maurolyci Abbati Messanensi Opuscula Mathematica. Liber primus, 161-210; Liber secundus, 211-262; Liber tertius, 263-285; apud Franciscum Franciscium Senensem, Venezia.
Menghini, M. (1982), Cavalieri e Leibniz: dagli indivisibili al differenziale: Montaldo, O. & Grugnetti, L. (a cura di), La storia delle matematiche in Italia, Università di Cagliari, Cagliari, 385-394.
Nobre, S. (a cura di) (1994), Meeting of the International Study Group on relations between history and pedagogy of mathematics, Blumenau, Brasile 25-27 luglio, UNESP.
Pepe, L. (1979), L’elemento primo dell’«Aritmetica razionale» di Pietro Mengoli, Bollettino U.M.I., 5, 16-A, 201-209.
Pepe, L. (1982), Note sulla diffusione della Géométrie di Descartes in Italia nel secolo xvii, Bollettino di Storia delle scienze matematiche, II.
Pepe, L. (1990), Storia e didattica della matematica: L’educazione matematica, III, I, 2, 23-33.
Piola, G. (1844), Elogio di Bonaventura Cavalieri, Bernardoni, Milano.
Riccardi, P. (1887-1890), Saggio di una Bibliografia Euclidea, Gamberini e Parmeggiani.
Riccardi, P. (1952), Biblioteca matematica italiana, Gorlich, Milano (ristampa).
Segre, B. (1958), La vita e l’opera di E. Torricelli, Archimede, 4.
Smith, D.E. (1959), A source book in Mathematics, Dover, New York (prima ed.: McGraw-Hill, 1929).
Speranza, F. (1994), A la recherche d’une philosophie de la mathématique idoine pour la didactique: Gagatsis, A. (1994), Histoire et enseignement des Mathématiques: Cahiers de didactique des Mathématiques, Thessaloniki, 14-15, 187-194.
Swetz, F.J. (1989), Using problems from the history of mathematics in classroom instruction: Mathematics teacher, 82, 370-377.
Swetz, F.J. (1995), To know and to teach: mathematical pedagogy from a historical context: Educational Studies in Mathematics, 29, 73-88.
Torricelli, E. (1644), Opera geometrica, Typ. A. Massae et L. de Landis, Firenze.
Ulivi, E. (1987), Le fonti di Bonaventura Cavalieri: la costruzione delle coniche fino allo Specchio Ustorio, Bollettino di Storia delle scienze matematiche, VII, 1, 117-119.
Vacca, G. (1915), Sulle scoperte di Pietro Mengoli, Atti dell’Accademia Nazionale dei Lincei (Cl. Sci. Fis. Mat. Natur.), 24, 508-513, 617-620.
Vacca, G. (1929), Apollonio, Enciclopedia Italiana, III, pp. 686-687, Istituto della Enciclopedia Italiana, Roma.
Valerio, L. (1661), De centro gravitatis solidorum libri tres, Dozza, Bologna (prima ed.: Roma 1604).
Van der Waerden, B.L. (1983), Geometry and Algebra in Ancient Civilizations, Springer Verlag, Berlin.
Weil, A. (1980), History of mathematics: why and how: Letho, O. (a cura di), Proceedings of International Congress of Mathematicians, Helsinki 1978, I, 227-236.
Back to the main page: è index.htm ç